Using multi-coefficient modeling to generate accurate time domain models
Promising high bandwidth and low power consumption combined with cost-effective manufacturing, integrated photonics has emerged as one of the key enablers of next-generation communications in everything from high capacity optical networks to board and chip-level interconnects. The technology is also showing promise in diagnostics and other health care related applications, environmental sensing, the internet of things (IoT), augmented and virtual reality (AR/VR), and quantum computing.
Figure 1: Integrated photonics technology is at the core of many emerging technology trends.
While the potential for integrated photonics is widely documented, design methodologies for reliable volume production are still in their infancy. To further increase adoption and enable integrated photonics to deliver low-cost volume production in applications like those in Figure 1, we need design tools and frameworks which enable first-time-right designs. Ensuring accurate device design prior to fabrication reduces the number of costly development cycles and improves time to market, often a critical competitive advantage in today’s fast moving technology sectors.
Today, photonic circuits consist of a relatively small number of individual building blocks such as couplers, waveguides, splitters, filters, reflectors, modulators and detectors. For most photonic building blocks, particularly passive elements, developing behavioral models or compact models for circuit simulation is straightforward [1].
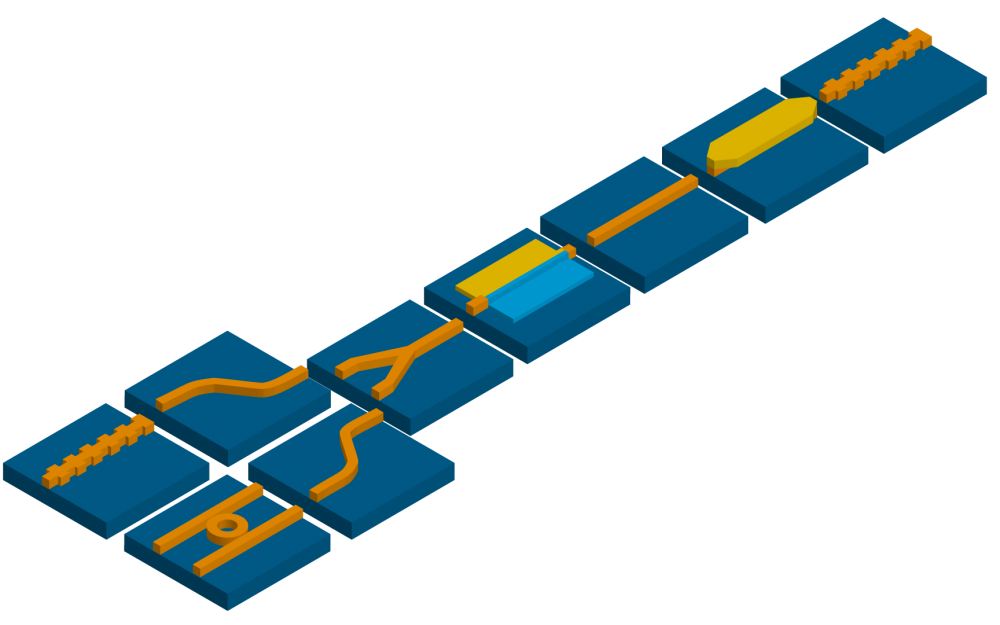
Figure 2: A simplified view of select photonic building blocks arranged as a DBR laser.
Modeling of active devices, in particular integrated lasers, remains a critical challenge. Unlike in III-V material systems, it is very challenging to create gain sections in silicon due to the indirect bandgap of silicon. Much research and development investment in methods of integrating gain media with silicon photonic circuits has been made over the years. Different approaches including multi-die designs, direct bonding, or growing secondary material systems on top of silicon are being researched to achieve the goal of tight integration of a light source with integrated photonics designs. In these architectures, the lasing cavity is part of the integrated circuit itself and the laser can no longer be understood as a discrete component. It becomes important to include laser models in comprehensive circuit simulations and design workflows. In these designs, one of the key performance characteristics to examine are reflections from the photonic integrated circuit back into the laser cavity. The effects of back reflections are particularly important in designs without optical isolation between the laser and integrated circuit as the reflections can degrade laser performance. To accurately capture the full dynamics of a laser including tunability, carrier and photon dynamics, a 1D travelling wave model is employed for the gain section of the laser. Figure 3 outlines how the model is employed to examine a self-consistent tunable hybrid laser cavity design consisting of passive and tunable waveguides, splitters, and Bragg gratings operating in connection with a III-V gain segment.
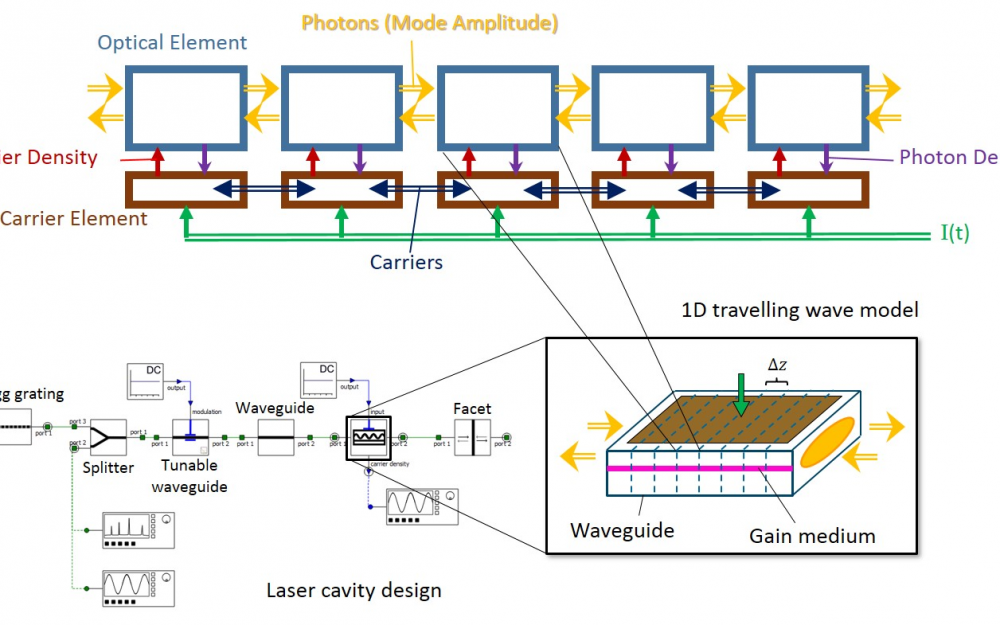
Figure 3: A 1D traveling wave model for laser cavity design and analysis
Time –domain laser modeling in 1D using an optical circuit simulator such as Lumerical’s INTERCONNECT requires accurate time-domain filtering in order to represent the frequency dependence of the material or modal gain. Additionally, the time domain filter must vary with the carrier density in the 1D spatial element. The filter therefore must replicate a family of gain spectrum curves varying according to the carrier density.
One approach would be to use a finite-impulse-response (FIR) filter and vary the filter coefficients with the carrier density such that the transfer functions of the filter match the gain curves at their respective carrier densities. Increased accuracy in the transfer function is achieved by increasing the number of filter taps. This approach presents challenges, as any FIR filter introduces delay (increasing with number of filter taps) which in turn affects the group delay which is a critical parameter in lasers and other resonant systems.
An alternative is to approximate the laser’s material or modal gain curve with a Lorentzian, which can be implemented as an infinite impulse response filter (IIR) in the time domain, fitted to the peak amplitude, peak frequency, and the width (or quality factor) of the experimental or theoretical gain curve family. The three Lorentzian fit parameters may be made to vary as a function of carrier density. This method faces challenges since the actual laser gain curves are not necessarily Lorentzian shaped even in the immediate vicinity of the gain curve peak where a simple Fabry-Perot laser would operate.
Another approach is to attempt to fit the gain curves in the vicinity of their peaks with other types of bandpass filters such as Bessel, Butterworth, or Chebyshev filters, and then use a bilinear transformation to generate discrete time IIR filters from continuous time filters, optionally employing frequency pre-warping. This approach does allow for more flexibility in the precise shape of the simulated gain curve however it is still not capable of providing accurate fits to arbitrary gain curve shapes.
When designing DFB, DBR, and more complex external cavity lasers, the lasing frequency is determined by the texturing and/or the resonances provided by the external cavities and not the peak of the laser gain curve. This allows for the fabrication and integration of lasers operating at different wavelengths merely by altering the external resonances without having to adjust the gain material (i.e., material system and quantum well structure). For designs where operating wavelength varies or where multiple lasers at different wavelengths are employed in a single system (e.g., a wavelength division multiplexed (WDM) telecommunication link) it is required that the arbitrarily shaped gain curves are approximated by an IIR time domain filter that is accurate over a broad frequency range.
To address the requirements of laser modeling in integrated photonics and the shortcomings of familiar methods outlined in this document, INTERCONNECT implements an extended variant of Lumerical’s proprietary multi-coefficient fitting algorithm to directly fit the required IIR time-domain filter impulse response spectrum to an arbitrarily shaped gain curve. The multi-coefficient model has also been extended to fit simultaneously to a family of gain curves that vary according to some scalar input parameter, such as carrier density in the case of laser modeling. The filter reproduces the target frequency responses at the corresponding values of the scalar parameters and interpolates the responses at intermediate values, as depicted in Figure 4. The target responses in Figure 3 are from gain curves reported by Ma et al. presented in [2].
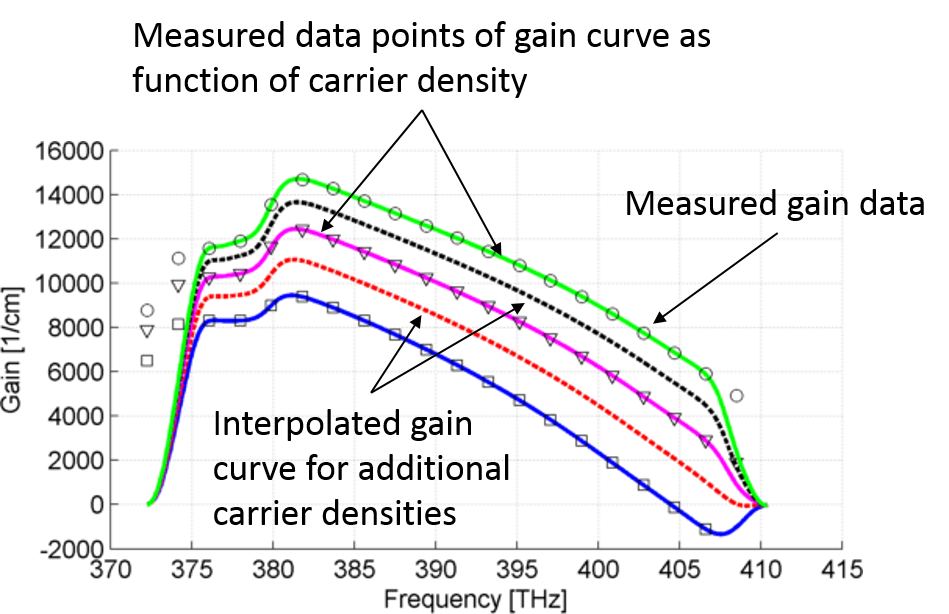
Figure 4: Lumerical’s gain curve fitting using an extended multi-coefficient model.
The ability to fit a time domain filter to an arbitrarily shaped frequency response is useful in many applications beyond fitting laser gain curves and laser modeling. The multi-coefficient fitting capability in Lumerical’s photonic circuit simulator, INTERCONNECT, is particularly useful to describe any linear optical or electrical component dependent on a single scalar control parameter using s-parameters (complex transmission coefficients). The multi coefficient fitting algorithm allows for the automatic generation of IIR filters resulting in more accurate time domain simulation by reducing the time delay errors introduced by FIR filters. This methodology can be used to model the effects of integrated lasers in integrated photonics designs and rapidly create time-domain elements in INTERCONNECT that can then be used to design, analyze and optimize complex photonic integrated circuits prior to fabrication.
References
[1] J. Pond et al., “A complete design flow for silicon photonics”, Proc. SPIE 9133, Silicon Photonics and Photonic Integrated Circuits IV, 913310 (1 May 2014); doi: 10.1117/12.2052050
[2] M-L Ma et al., “Measurement of gain characteristics of semiconductor lasers by amplified spontaneous emission from dual facets”, Optics Express, Vol. 21, No. 8, p.10335, OSA 2013

