Enabling broadband design through new approaches to material modeling
With improvements to algorithm architecture and computing technologies boosting the speed of the finite-difference time-domain (FDTD) technique, it is increasingly applied to a diverse range of application areas. Part of the appeal of FDTD is that, as a time-domain technique, a single simulation can be used to provide simulation results at many frequency points. While this appears to provide the ability to analyze and optimize device design across a wide wavelength range, this is only true to the extent that the models used to describe the dispersive nature of the constituent materials are themselves accurate over the wavelength range of interest. A significant multi-wavelength challenge results from the fact that accurate broadband simulation requires accurate broadband material models that are computationally efficient.
The traditional approach to FDTD material modeling
To account for the dispersive nature of optical materials, FDTD simulators typically employ Drude, Debye, or Lorentz materials (see Figure 1). Originally derived from simplified models of the permittivity of idealized materials, these models offer good insight into the behavior of optical materials through their characteristic shapes (see Figure 2), but fail to accurately capture the dispersive properties of real materials. The dispersion of real materials is impacted by impurities, defects, and other more complicated material issues that invalidate the assumptions of these idealized materials.
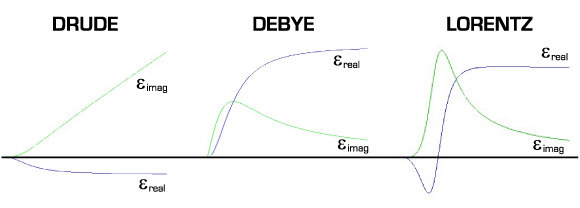
Figure 1: Characteristic complex permittivity curves of Drude, Debye, and Lorentz materials.
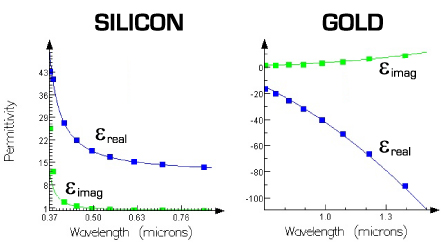
Figure 2: Lorentz model fit to Silicon across the visible, and a Drude model fit to Gold in the near infrared. Material data is from Palik’s Handbook of Optical Constants (Vol. 1 and 3) and the CRC Handbook of Chemistry and Physics, respectively, for silicon and gold.
To address the above limitations, some device simulators employ combined Lorentz/Drude/Debye models (for example, a Lorentz-Drude dispersion model) or multipole models (e.g. a multipole Lorentz model, which is a dispersion model that results from combining two or more distinct Lorentz models). While this provides more degrees of freedom to fit the observed material dispersion, this approach is hindered as it must still make use of the three available models with their characteristic shapes shown above in Figure 1. Some materials are just not naturally described by Lorentz, Drude or Debye materials – witness the color filters that are routinely used within CMOS image sensors, or many of the organic compounds within OLED structures. Even with the favored approach of using a Lorentz-Drude model to describe gold, significant deviations between the fit and the experimental data exist over the visible (see Figure 3).
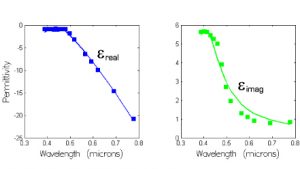
Figure 3: Lorentz-Drude model fit to Gold over the visible from 380 to 780nm; complex fit provides an RMS error of 2.015, with much of the deviation originating from the discrepancies seen in the imaginary permittivity fit. Material data was obtained from the CRC Handbook of Chemistry and Physics.
While it is true that, with enough terms it is possible to recreate any dispersion profile, there is an increased cost in terms of slower computation speeds by relying on more terms. The fact that with many simulators the types and number of terms are chosen by hand makes the process cumbersome and inefficient. The result: the end user chooses not enough terms and model accuracy suffers, or too many terms and computation speed slows. Choosing the correct number of appropriate terms in an expedient manner remains the key to overcoming the multi-wavelength challenge.
A better approach: multi-coefficient models (MCMs)
To overcome the multi-wavelength challenge, Lumerical has pioneered the introduction of multi-coefficient materials (MCMs). MCMs rely on a more extensive set of basis functions to better fit dispersion profiles that are not easily described by Drude, Debye, and Lorentz materials. MCMs can also be generated instantaneously at the touch of a button to provide designers with the ability to automatically and optimally choose the type and number of terms required to accurately describe their materials. The type of fit that can be automatically generated to imported material data is shown for gold below in Figure 4. With a comparable cost in model complexity and computation speed, the resulting MCM model is superior to the Lorentz-Drude model as shown.
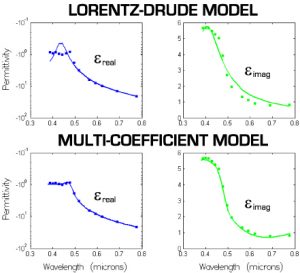
Figure 4: Comparison of Lorentz-Drude model to the multi-coefficient model (MCM) of comparable computational cost. The MCM provides a much better description of material dispersion as evidenced by the reduced RMS error 0.137 compared the RMS error of 2.015 for the Lorentz-Drude model. The real permittivities (shown in blue) are plotted on a logarithmic scale because of the wide variation in permittivity values over the visible wavelength range.
Able to generate highly-accurate material models on their own, designers can better address proprietary designs which employ refractive index data measured from devices made with their chosen industrial process. This promises to increase the reach of time-domain simulators across the frequency spectrum at the expense of methods which require multiple simulations, each performed at a distinct operating frequency.

